


 |
 |
 |
![]() Introduction
Introduction
![]() Hypothesis
Hypothesis
![]() Requirements
Requirements
![]() Points
to consider
Points
to consider
![]() Gathering
the Data
Gathering
the Data
![]() Presenting
the Data
Presenting
the Data
![]() Getting
results
Getting
results
![]() Important
notes
Important
notes
What is the chi square test?
The chi square test is used to test a distribution observed in the field against another distribution determined by a null hypothesis.
Being a statistical test, chi square can be expressed as a formula. When written in mathematical notation the formula looks like this :
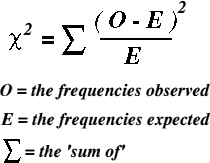
When using the chi square test, the researcher needs a clear idea of what is being investigating. It is customary to define the object of the research by writing an hypothesis. Chi square is then used to either prove or disprove the hypothesis.
Prior to using the chi square test there are certain requirements that must be met. These are :-
The hypothesis is the most important part of a research project. It states exactly what the researcher is trying to establish. It must be written in a clear and concise way so that other people can easily understand the aims of the research project.
Using an example of agriculture and rock type, the hypothesis might be written like this.
The frequency of farms depending mainly upon cereal crops for an income is not related to underlying rock type.
Note that the hypothesis states that there will be no significant relationship between rock type and the frequency of farms depending upon cereal growth for an income. Such an hypothesis is called a 'null hypothesis', often referred to as H0. This is the way in which an hypothesis should always be written when conducting research. The opposite, or H1 hypothesis states that there is a significant relationship between one rock type and another in the number of farms relying mainly on growing cereal crops.
A well written hypothesis is essential. If you are not clear about your aims, you wont know what data you need to collect. There is nothing worse than finding that half the data you need was never collected ! Not only will you have to go out and do all the data collecting again, you will also find that you project takes twice as long as you expected.
The whole purpose of the research project should now concentrate upon testing you hypothesis. It is not necessary to end up with the result you expect to find. Any result, even an inconclusive one is valid. The results should set you thinking about "why?" . That is the whole purpose of research.
Having decided upon the wording of the hypothesis, the researcher should consider whether there are any other factors that may influence the study.
Considering our example of rock type and farm dependence on cereal crops, the following additional factors might be considered. This is not a full list, but a group of suggested factors that could influence the results of the study.
a) Do some farmers treat the soil to redress mineral or pH problems, or add drainage or irrigation to the fields? If they do, then the farmer is no longer growing crops on the pure underlying rock type.
b) Are farmers bound or enticed by any legislation that prohibits their free choice of farming policy, such as grants or penalties for practising certain types of farming?
c) Are the farms gaining an income from successful growth of cereal crops or from subsidies that make up a shortfall in successful crop growth?
The researcher should mention these possible problems in their project, and explain how they could have influenced the results obtained. In some cases the researcher may decide to take steps to reduce outside factors influencing the result, depending upon the hypothesis being tested.
Before starting to gather data be sure you know exactly what you need to record. Decide upon a way in which you will write down your results and make sure that you do write them down immediately. Don't rely on memory - it isn't worth it, especially when dealing with numbers.
Once the researcher has selected a research site, he / she can start to collect data, visiting all the farms in the selected area and dividing them into farms that rely on cereals and those which do not. Farms which derive 75 percent or more of their income from cereals might be regarded as dependant on cereal production; those which derive 74 percent or less of their income in this way may be considered as not being dependant on cereal production.
Data in the form of numbers ( numerical data ) can be presented as either graphs or tables.
When using chi square the data is presented as a table. It is a good idea to prepare an empty table before you start to do any calculating. That way, you can enter your calculations straight into the table as you do them. You thus save time and avoid making mistakes.
The tables below shows how the original observations might appear for our rock type / cereal crops example.
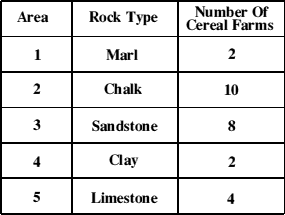
1) Observed Frequency : This is the number of cereal dependant farms that were found located on each of the rock types. If the total number of cereal dependant farms found on Chalk was 10, the number 10 would be entered in the table next to 'Chalk'. The same is done with the number of cereal dependant farms found on each of the other rock types.
2) Expected Frequency : Remember that our hypothesis states that rock type has no effect upon the distribution of farms that draw their main income from growing cereal crops? Well, if that is true, then it would seem reasonable to assume that we should find a roughly even distribution of such farms regardless of the underlying rock type. To find our expected frequencies we need to find the number of these farms we would expect to find in each area if they were distributed evenly. In our example we have 26 farms spread over 5 equal sized areas of different rock types, so the expected frequency is 26/5, or 5.2
3) Observed minus Expected : Just as it seems, the expected frequency is subtracted from the observed one. This may produce a negative number. It doesn't matter at this stage because the chi square test will take account of this!
4) (Observed minus Expected)² : Take the value from step (3) and square it. (This will remove any negative numbers).
5) (Observed - Expected)² / Expected : Take the value from stage (4) and divide it by the value from stage (2).
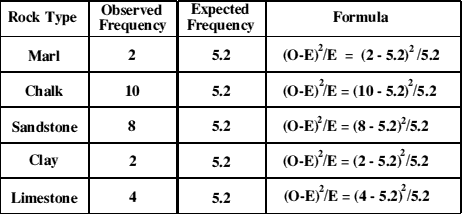
Chi - Square equals all the sum of the values for stage (5), so we have......
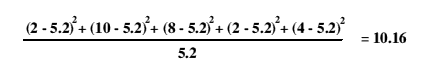
This value doesn't mean much on its own. It must be looked up in a table of chi - square critical values to show us the extent to which the relationship we are testing might be due to chance.
A table of chi square values will show 'critical values' and degrees of freedom.
The degree of freedom is found by subtracting 1 (one) from the total number of categories in the study. In this case there are five categories of rock types so the degrees of freedom are 5 - 1 = 4.
A table of critical values for chi square shows that with four degrees of freedom the critical value of chi square is 9.49 at the 0.05 level of significance. Our calculated value of chi square is 10.16. This is larger than the critical value at the 0.05 level so it indicates that there is less than 5 percent probability that the relationship we have tested is random. In other words, we might expect such a distribution to occur purely by chance less than five times in every hundred.
We can, in consequence, reject the null hypothesis and conclude that on the evidence we have collected the reliance on cereal production as a main source of income is affected by rock type.
The null hypothesis ( H0) states that the relationship you have been studying DOES NOT EXIST. If the hypothesis is rejected , then the relationship DOES EXIST.
We value
your ideas and suggestions. Please contact the
maintainer of this site.
This page
can be found at: http://www.geography-site.co.uk
Last update to
this statement was on:
February 20, 2006
© Copyright Geography Site